[10000ダウンロード済み√] (x y z)^3-x^3-y^3-z^3 106226-(x+y+z)(x^2+y^2+z^2-xy-yz-zx)=x^3+y^3+z^3-3xyz
Pascal's (or Tartaglia's) Tetrahedron the left outline is a binomial expansion of $(xy)^3$, while the right outline is a binomial expansion of $(xz)^3$ and the bottom outline is a binomial expansion of $(yz)^3$
(x+y+z)(x^2+y^2+z^2-xy-yz-zx)=x^3+y^3+z^3-3xyz-Y = 5 3x – 4y = 14 5 x = 4;Get stepbystep solutions from expert tutors as fast as 1530 minutes Your first 5 questions are on us!
(x+y+z)(x^2+y^2+z^2-xy-yz-zx)=x^3+y^3+z^3-3xyzのギャラリー
各画像をクリックすると、ダウンロードまたは拡大表示できます
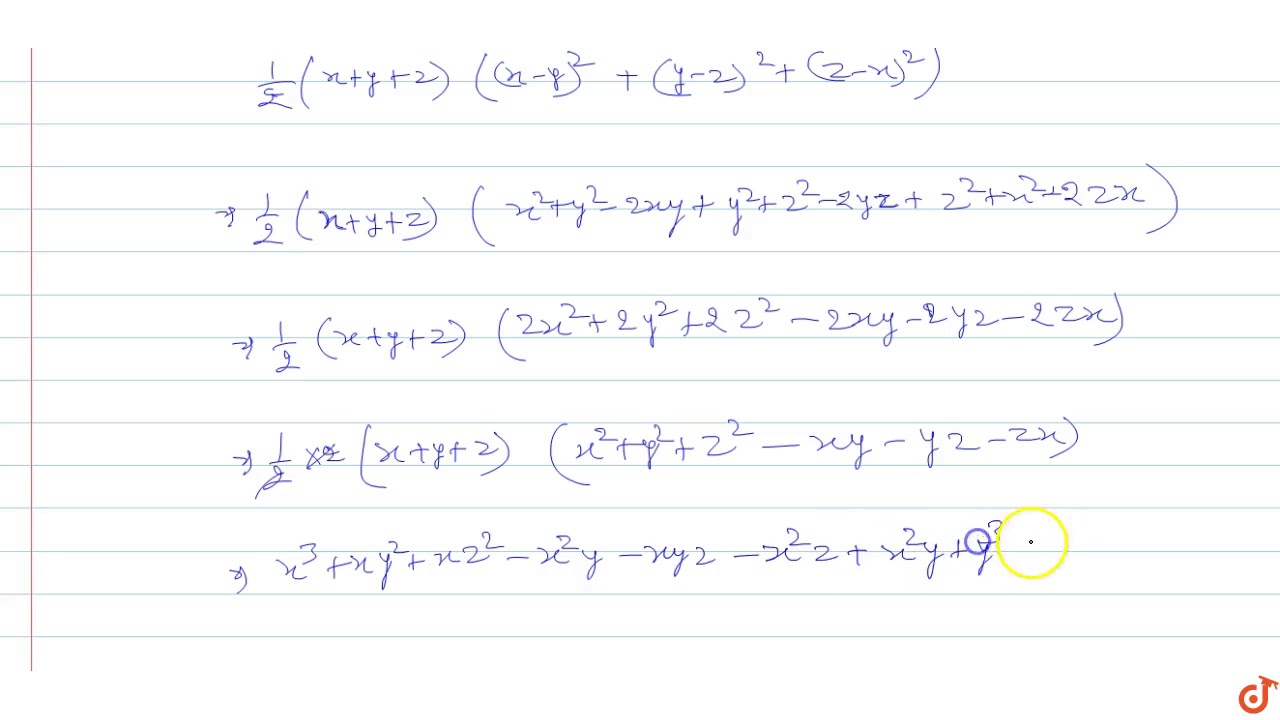 |  |  |
 | ||
 |  |  |
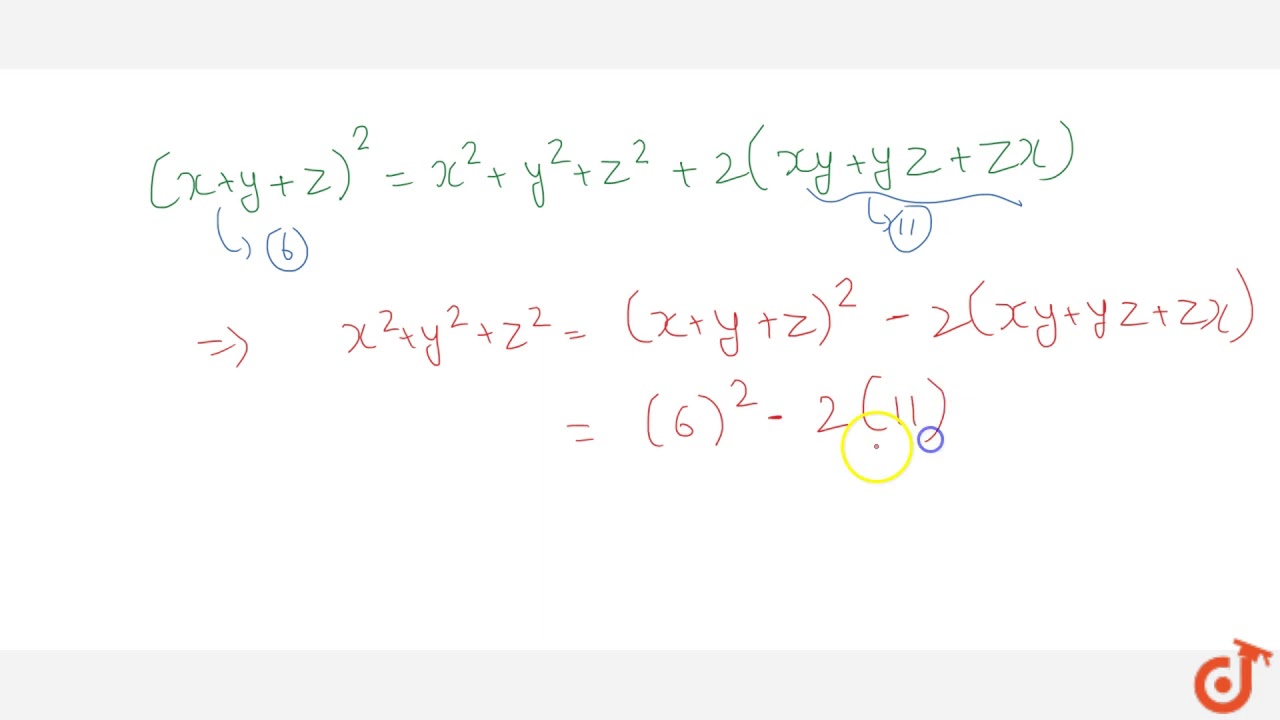 |  | |
「(x+y+z)(x^2+y^2+z^2-xy-yz-zx)=x^3+y^3+z^3-3xyz」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 | 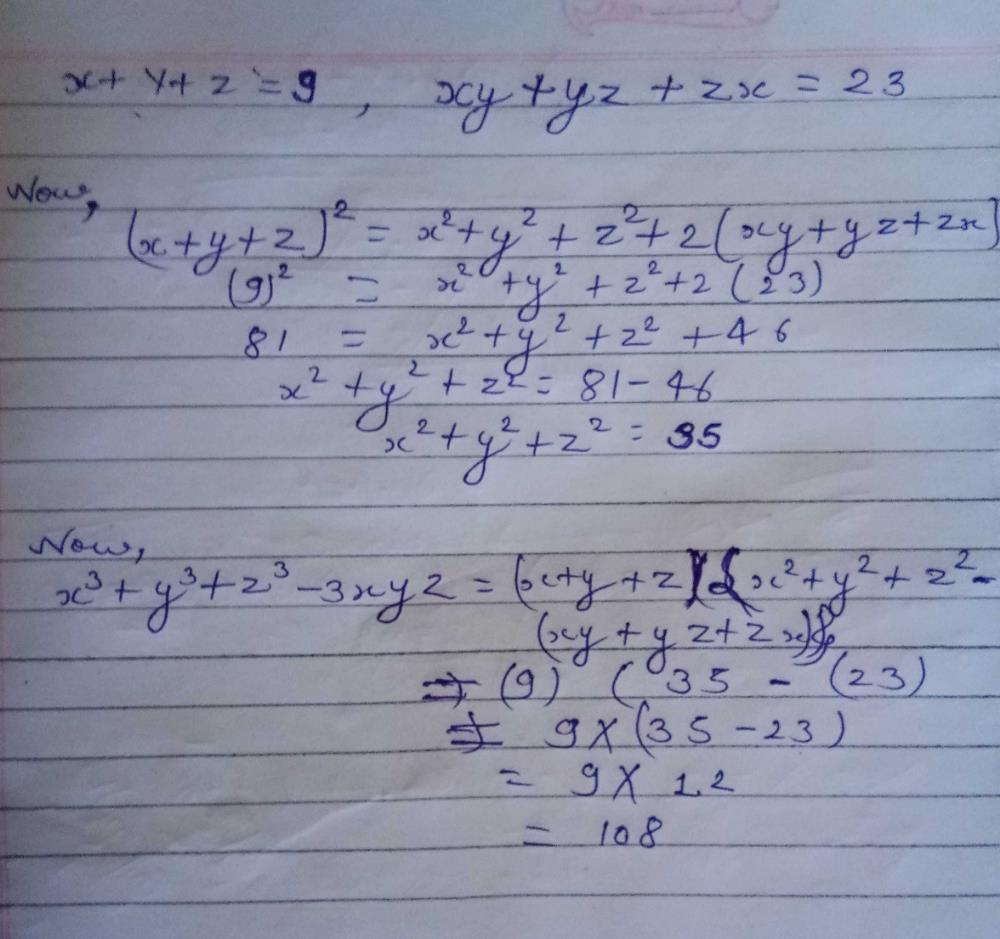 | |
 |  | |
 |  |  |
「(x+y+z)(x^2+y^2+z^2-xy-yz-zx)=x^3+y^3+z^3-3xyz」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 | ||
 | ||
 | 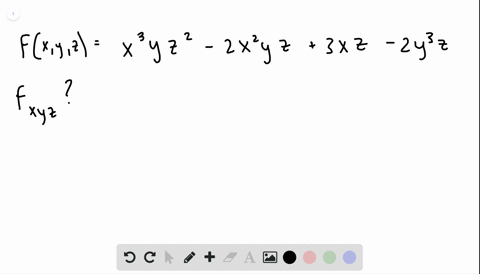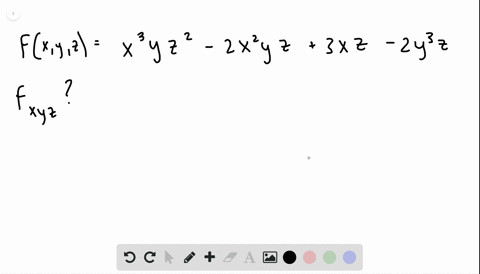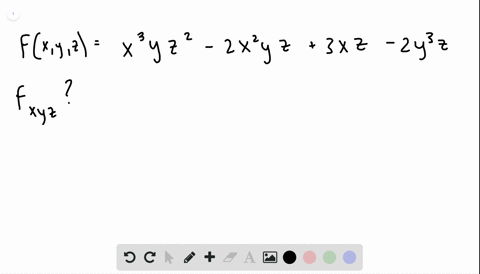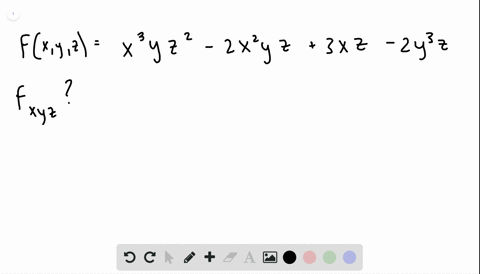 | |
「(x+y+z)(x^2+y^2+z^2-xy-yz-zx)=x^3+y^3+z^3-3xyz」の画像ギャラリー、詳細は各画像をクリックしてください。
 | 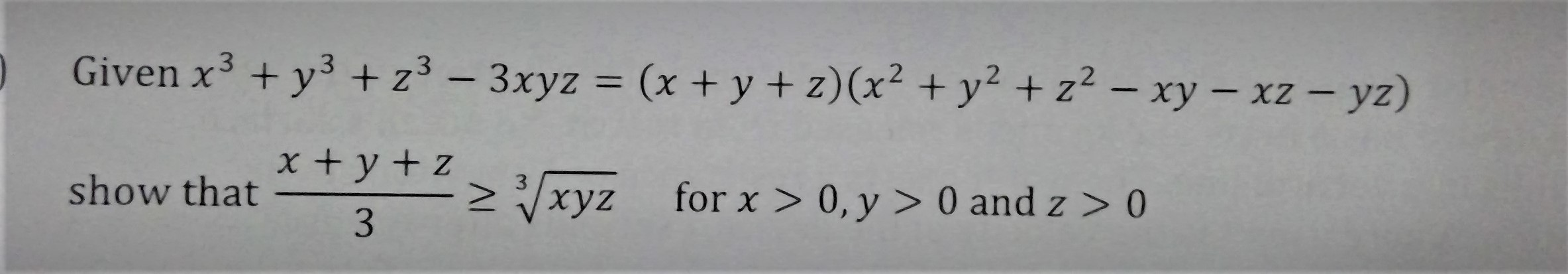 |  |
 |  |  |
 |  |  |
 |  | |
「(x+y+z)(x^2+y^2+z^2-xy-yz-zx)=x^3+y^3+z^3-3xyz」の画像ギャラリー、詳細は各画像をクリックしてください。
 | 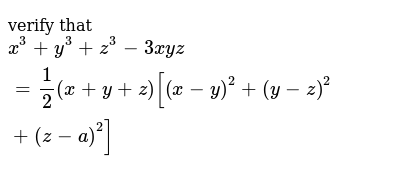 | |
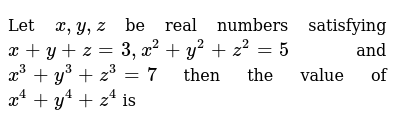 |  |  |
 |  | 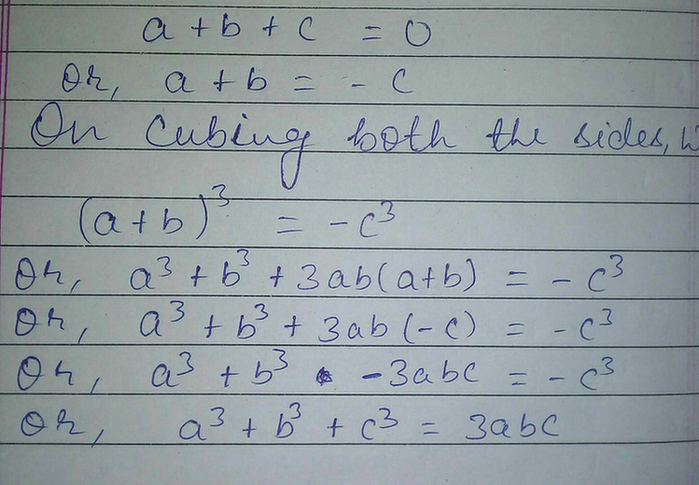 |
 |  | 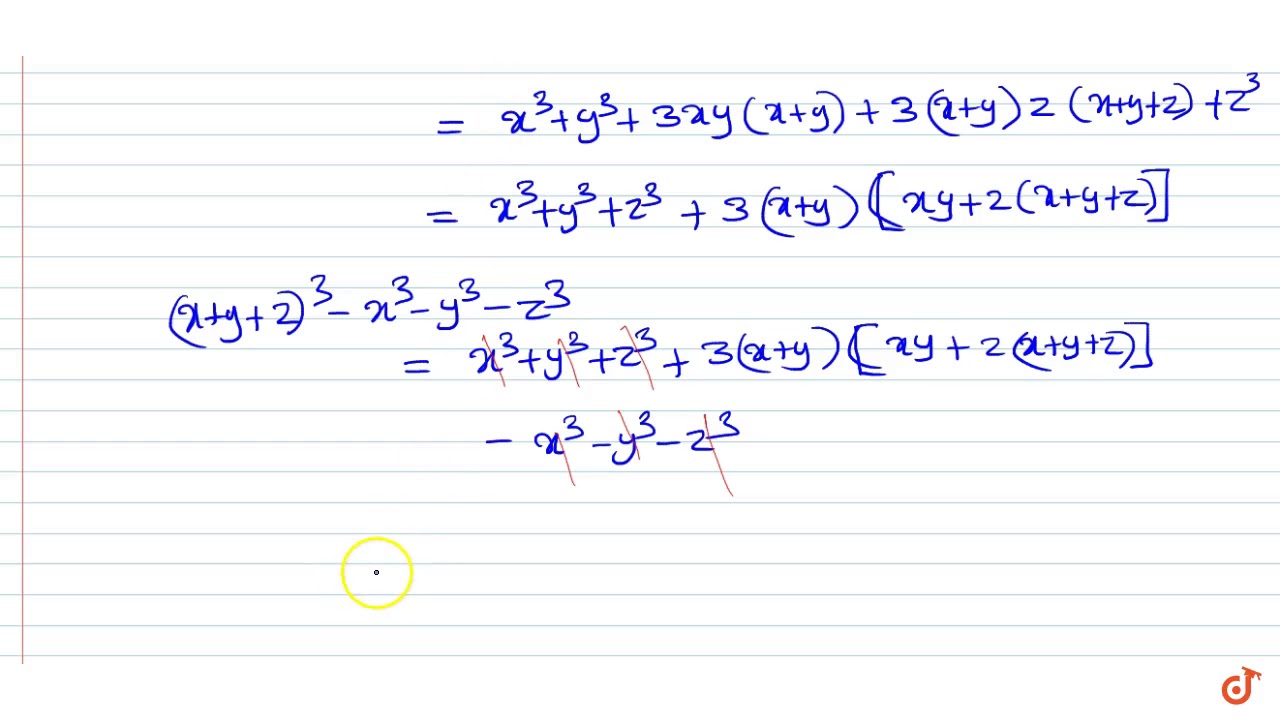 |
「(x+y+z)(x^2+y^2+z^2-xy-yz-zx)=x^3+y^3+z^3-3xyz」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
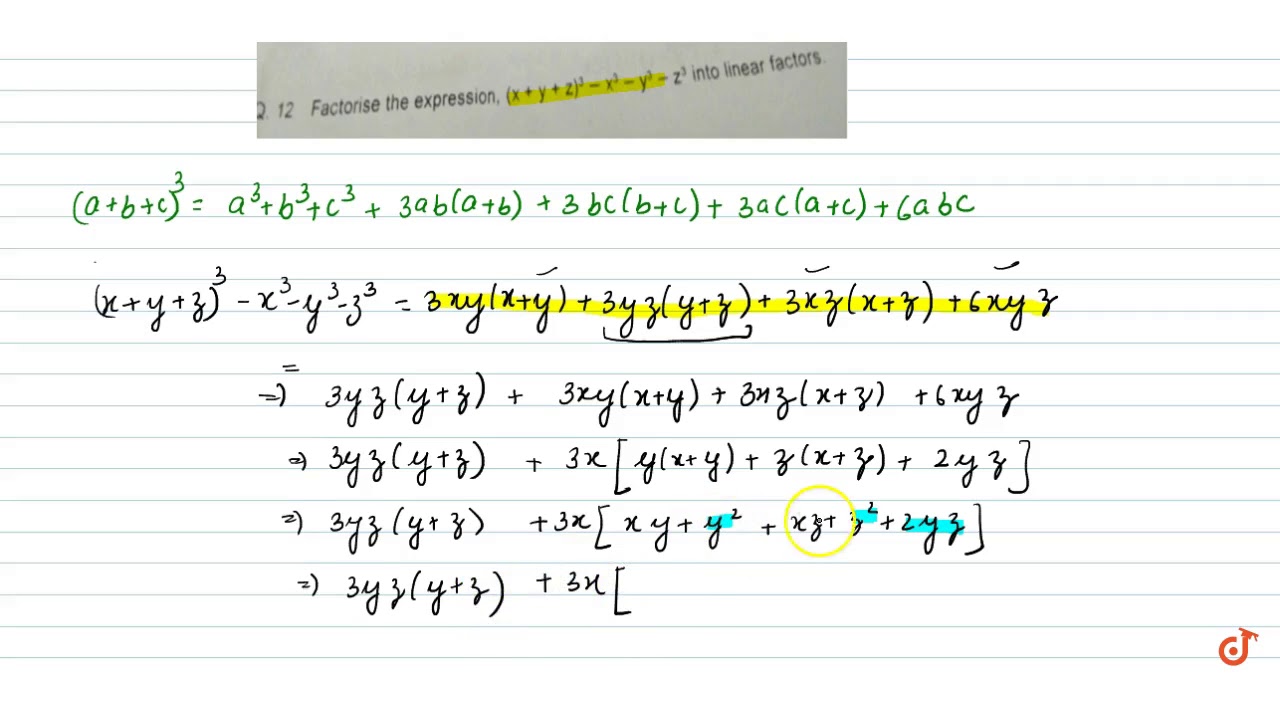 |  |  |
 |  | |
 |  |  |
「(x+y+z)(x^2+y^2+z^2-xy-yz-zx)=x^3+y^3+z^3-3xyz」の画像ギャラリー、詳細は各画像をクリックしてください。
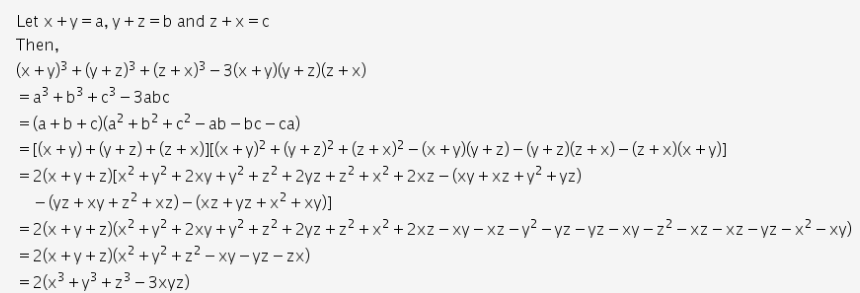 |  |  |
 |  |  |
 | ||
 |  |  |
「(x+y+z)(x^2+y^2+z^2-xy-yz-zx)=x^3+y^3+z^3-3xyz」の画像ギャラリー、詳細は各画像をクリックしてください。
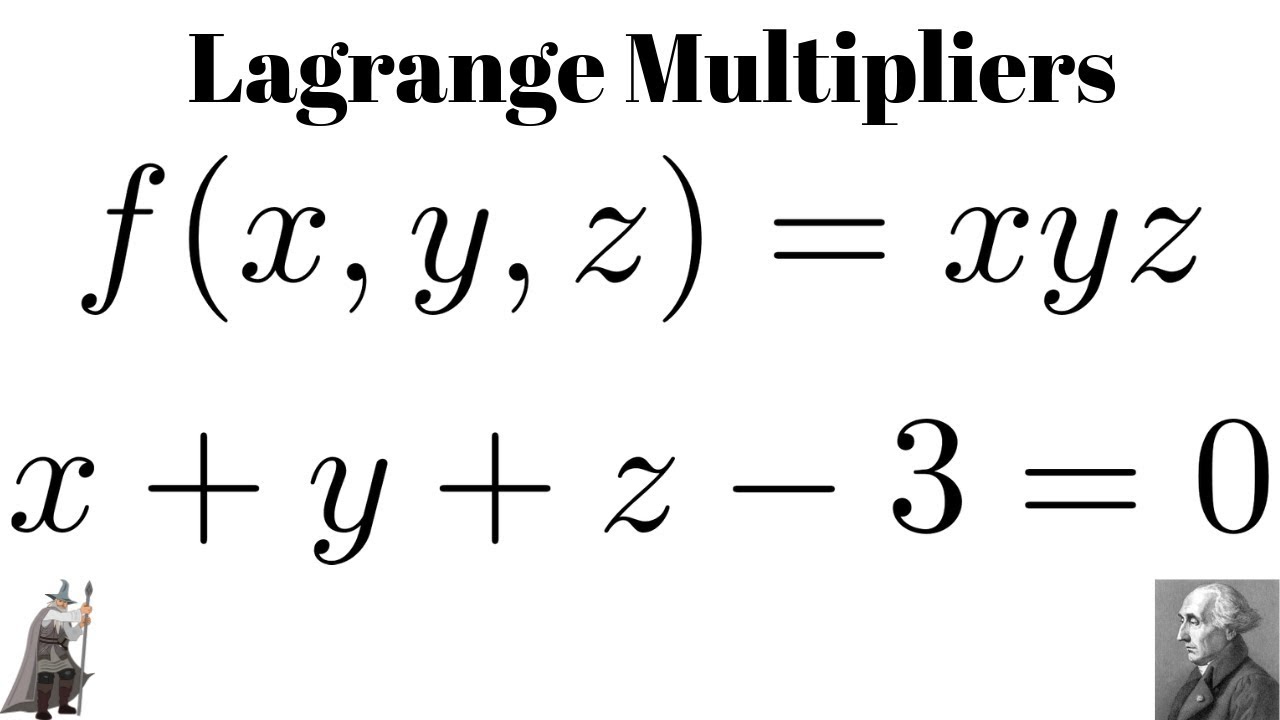 |  |  |
 | 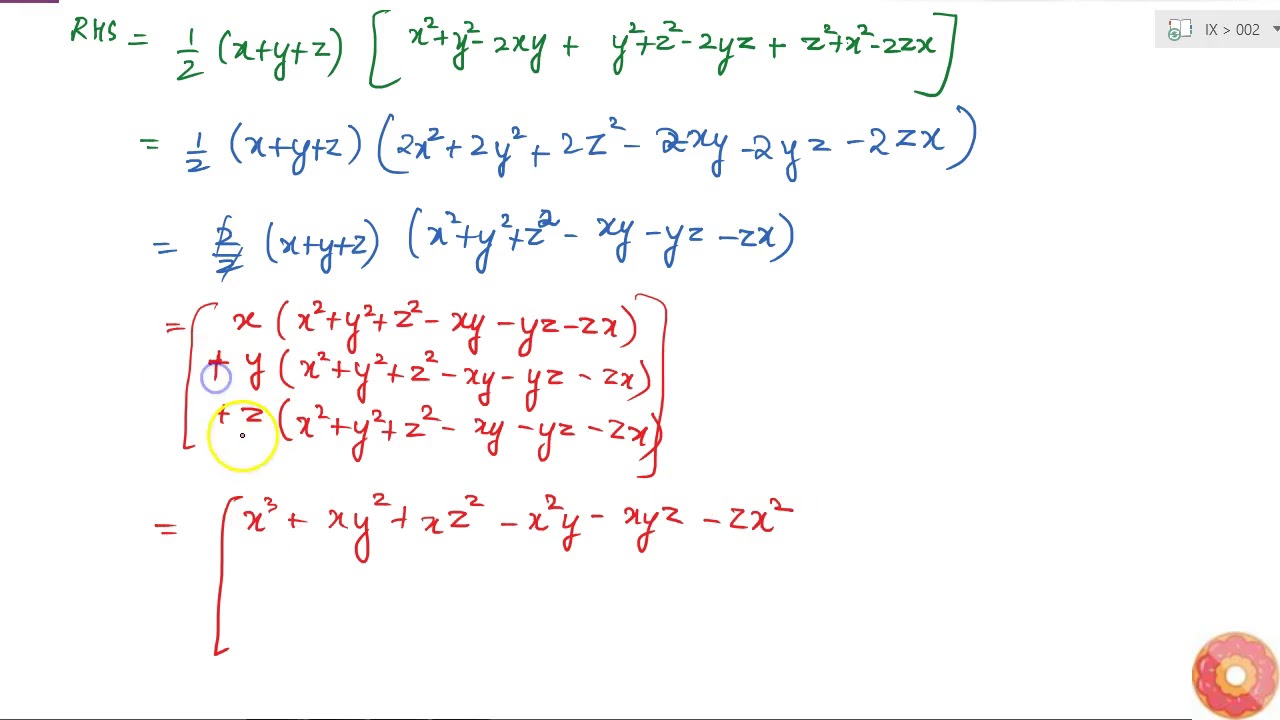 | 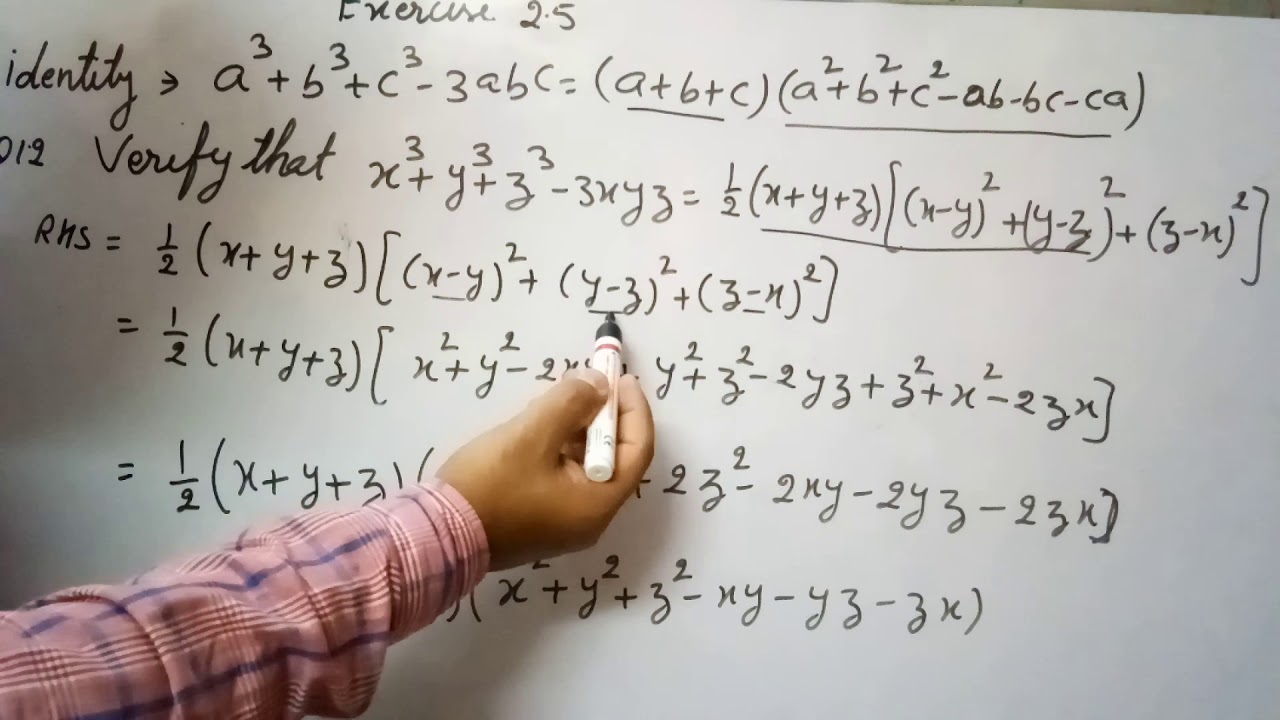 |
 |  |  |
 |  |  |
「(x+y+z)(x^2+y^2+z^2-xy-yz-zx)=x^3+y^3+z^3-3xyz」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  |
View Full Answer Deep Sah, added an answer, on 3/10/15 Deep Sah answered this We know that a^3 b^3 c^3 3abc = (a b c) (a^2 b^2 c^2 ab bc ac) Take, a = xy, b = yz, c = zx we get, (xy)^3 (yz)^3 (zx)^3 3 (xy) (yz) (zx) factorise 8x*3y*327z*318xyz if x1/x=5,then find value of x^31/x^3 The valuesof 249square 248square is 729X3512y3 Factorise (abc)³a³b³c3 I need very urgently please answer as quickly as you can Rich Text Editor, question_data Editor toolbars Basic Styles Bold Paragraph Insert/Remove Numbered List Insert/Remove Bulleted
Incoming Term: (x+y+z)^3-x^3-y^3-z^3, x+y+z=0 x^3+y^3+z^3=3xyz, 3^x=4^y=12^-z find 3/x+3/y+3/z, x+y+z=3 x^2+y^2+z^2=3 x^3+y^3+z^3=3, x+y+z=1 x^2+y^2+z^2=2 x^3+y^3+z^3=3, (x/2+y+z/3)^3+(x/3-2y/3+z)^3+(-5x/6-y/3-4z/3)^3, if x^3+y^3+z^3=3xyz then x+y+z=, if x+y+z=9 and x^2+y^2+z^2=35 find x^3+y^3+z^3-3xyz, (x+y+z)(x^2+y^2+z^2-xy-yz-zx)=x^3+y^3+z^3-3xyz, what is x^3+y^3,




コメント
コメントを投稿